
いろいろな正多角形をかいてみよう 家庭学習レシピ
Web〈正多角形の対角線の求め方〉 正n角形=(n3)×n÷2 よって、 正八角形=()×8÷2=本 正十七角形=(173)×17÷2=119本 となると思います。 ClearnoteでできることWeb正24 角形や正36 角形においても,正18 角形と同様に4 本以上の対角線が集まる点が見られ るが,他の「普通の点」にまぎれていて,「多くある」という印象はない。 対角線の交点に関す

いろいろな正多角形をかいてみよう 家庭学習レシピ
Web〈正多角形の対角線の求め方〉 正n角形=(n3)×n÷2 よって、 正八角形=()×8÷2=本 正十七角形=(173)×17÷2=119本 となると思います。 ClearnoteでできることWeb正24 角形や正36 角形においても,正18 角形と同様に4 本以上の対角線が集まる点が見られ るが,他の「普通の点」にまぎれていて,「多くある」という印象はない。 対角線の交点に関す
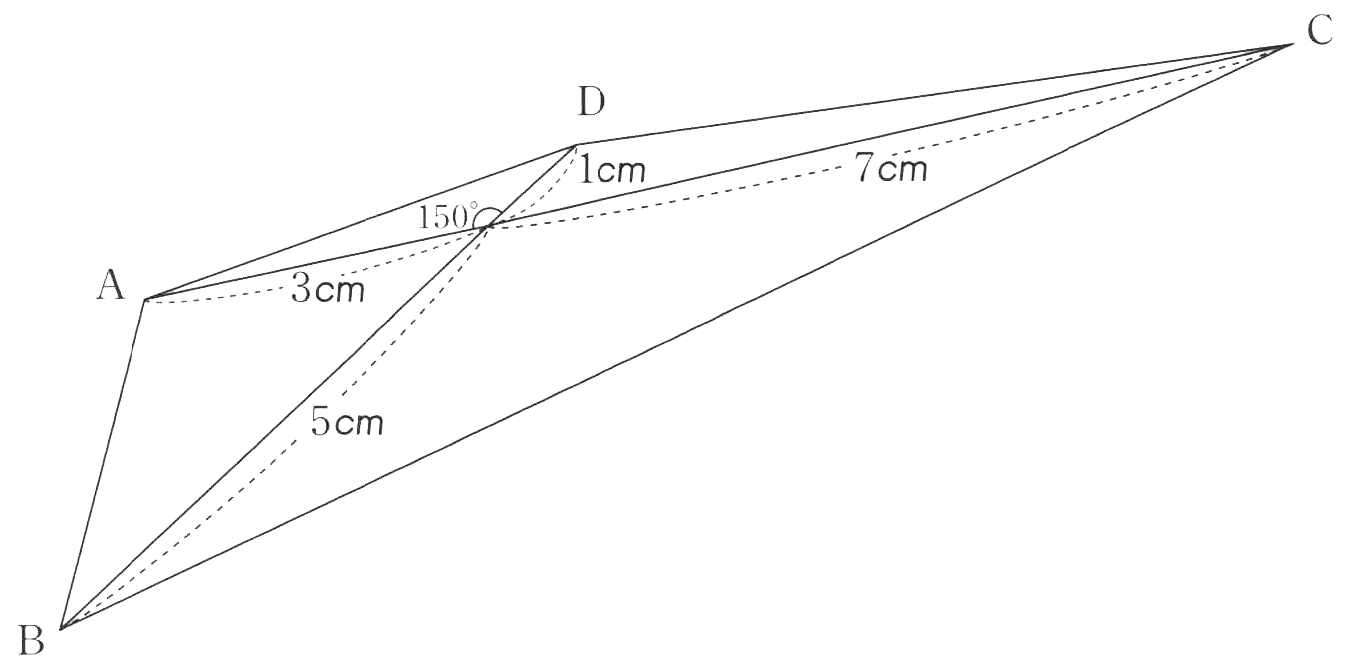
四角形の面積 フェリス女学院17 ジーニアス 中学受験専門塾
四角形の2つの対角線のなす角が90°の場合 左図の四角形ABCD(たこ形)の面積Sは、 BD AC 2 1 S です。 (面積)=(対角線)×(対角線)÷2 です。 しかし、ややイメージがわきにくいようです。 そこで、左図のように、 BDに平行で点Aを通る直線,点Cを通る直線, ACに平行で点Bを通る直線,点Dを通る直線 を引き、水色の長方形を考えれば、 四角形ABCDの面積は、 水色の長方形の面積の半分となり 円に内接する四角形・外接する四角形の性質はたくさんあります。それらをまとめてみました。 ab=a,bc=b,cd=c,da=dとする。また四角形abcdの対角線acとcdの交点をeとする。 単に∠aなどとかいたときは四角形の内角とする。 円に外接する四角形(内接円が存在)
